Simple bag-of-words loop closure for visual SLAM

Edit: I added some code and info on the precision-recall curve that is usually used to evaluate this sort of classification algorithms.

This post goes through the theory and implementation of a simple algorithm for loop closure detection in visual SLAM. The code is available on my Github.

As part of my research in using deep learning for SLAM, I found that loop closure detection would be a promising first application, due to its similarity to well-studied image classification problems. Before going ahead, I wanted to implement a baseline solution using "conventional" computer vision techniques. The following post describes the code I ended up implementing, based on the image description subsystem in ORB-SLAM2.

Goals

The main goal in loop closure is being able to detect when the robot is observing a previously-explored scene, so that additional constraints can be added to the map. As the number of frames grows, the naive solution quickly becomes computationally intractable. Instead of directly comparing pixel values, a better idea is to build a compact description of each scene that can be handled faster.

Building a compact vector representation for images.

AThese descriptions should be designed so that vector distance in the descriptions space is equivalent to similarity in the image space. For optimum performance, the vectors should also be robust to illumination or slight viewpoint changes.

There's also a huge body of work on data structures that can be used to efficiently query vector descriptors. We won't be covering those here, since these techniques are applicable to any image descriptor.

To recap, we are looking for the following properties:

descriptors should be quick to compute and take up little memory;
distance in the descriptors vector space should map to image similarity, so that similar scenes can be found by simply computing the vector distance;
descriptors should be robust under illumination or viewpoint changes.

Bag of words representations

We start by picking hundreds of interest points (features) throughout the image and extracting their representations using one of the available feature descriptors. For this, we can use the SURF descriptor available in OpenCV:


// This vector will hold the detected keypoints
vector<cv::KeyPoint> keypoints;

// This vector will hold their vector descriptors
vector<float> descriptors;

surf_detector->detectAndCompute(
	image, cv::Mat(), keypoints, descriptors);

Directly using the vector<float> as the image representation is not a good idea, since it takes up a lot of space and does not generalize well to new images. To compress it, we borrow an idea from text processing: the (Visual) Bag of Words (BoW) representation. First, he feature descriptors are clustered around the words in a visual vocabulary. The clustering reduces the problem to a matter of counting how many times each word in the vocabulary occurs in the original vector<float>. Finally, the image can be represented using the resulting histogram of frequencies, as shown in the following diagram:

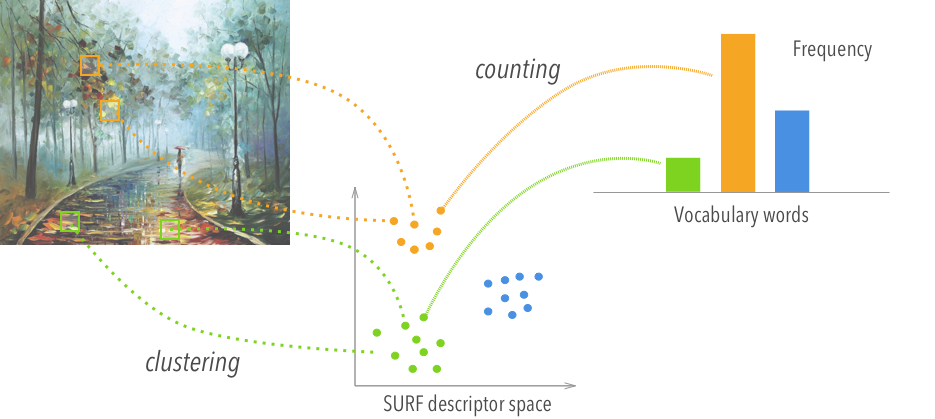
The vocabulary is trained beforehand using k-means clustering and a large dataset of images.

Testing on a real dataset

The "New College" dataset from the authors of FAB-MAP is a great dataset to use for benchmarking SLAM loop closure, since it provides ground-truth scene correspondences kindly contributed by humans.

For the implementation, I've used OpenCV and the DBoW2 library that's also used by ORB-SLAM2. I've set up a simple C++ project here that loads the images and computes the image-level similarity.

To compare the performance of the program to ground-truth, we can define a confusion matrix, whose element $i,j$ is defined as the vector distance between the representations of images $i$ and $j$. Small values of $C_{i,j}$ mean that the images $i$ and $j$ are similar and thus potential loop closure candidates. That's what we get by plotting the confusion matrices side by side:

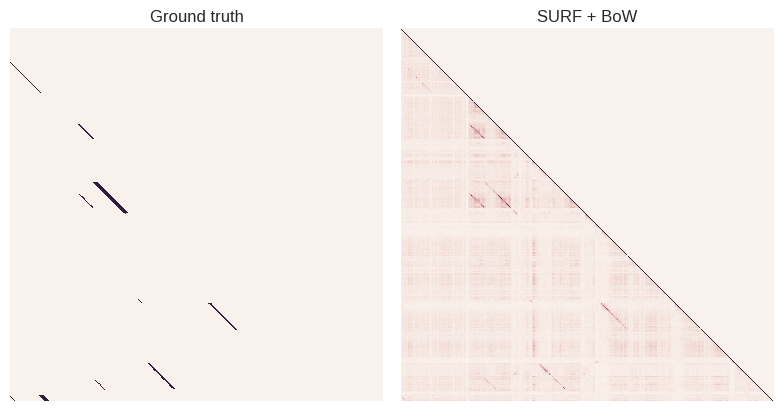
Confusion matrix compared to ground truth

As expected, the BoW-based confusion matrix is fuzzier than the binary ground-truth, but still matches quite well. In real applications, these raw scores would be post-processed to reduce false positives. For example, geometric and visibility constraints can be used to exclude some candidates and improve the reliability of the system. These techniques can be applied to any descriptor though, so discussing them is out of topic when it comes to BoW representations.

The precision-recall curve

Watching fuzzy dots on an heatmap is obviously not the best way to evaluate loop closure. Since loop closure can naturally be framed as a classification problem, we can plot a precision-recall curve (PR curve) to better quantify the performance of the system.

The PR curve highlights the tradeoff between precision (absence of false positives in the detection) and recall (prediction power). As expected, tweaking the algorithm to improve recall usually leads to more false positives due to the increased sensitivity to similarities in the image.

In the context of loop closure, these quantities can be computed as follows:

$$ \textrm{precision} = \frac{\textrm{Number of correctly detected closures}}{\textrm{Number of reported closures}} $$

$$ \textrm{recall} = \frac{\textrm{Number of correctly detected closures}}{\textrm{True number of closures in the ground truth}} $$

Precision and recall are usually plotted on the x and y axes of a scatter plot to highlight their inverse relationship:

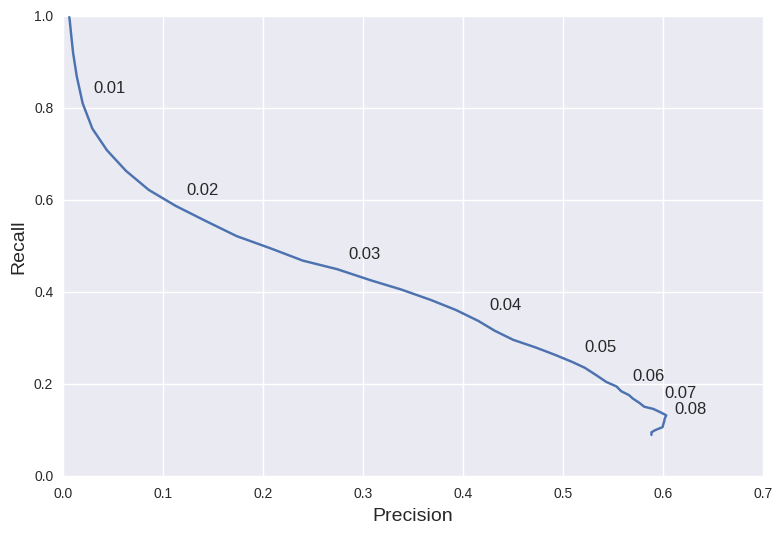
Precision-recall curve for the BoW approach

In this case, I explored the PR tradeoff by changing the threshold value applied to the scalar distance computed between BoW representations. Lowering the threshold makes the system more liberal in reporting loop closures, leading to higher recall but correspondingly low precision (loads of false positives).

Conclusions

This simple vision-only system performs pretty badly and would definitely need help from geometric and temporal constraints to use in a real SLAM system. However, it will be an useful benchmark for further research.